PELABELAN TOTAL SUPER (a,d) SISI ANTIMAGIC PADA GRAF TUNAS KELAPA TUNGGAL
Isnawati Lujeng Lestari, Dafik, Susi Setiawani
Mathematics Education Department
FKIP University of Jember
Abstrak. Graf G dengan jumlah titik p dan sisi q memiliki pelabelan total (a,d) jika ada fungsi bijektif f : V(G)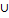
E(G) 
{1,2,…,p+q} sedemikian hingga bobot sisi, w(uv)=f(u)+f(v)+f(uv), uv 
E(G), membentuk barisan aritmatik dengan suku pertama a dan selisih tiap suku d. Suatu graf G adalah super jika label terkecil yang mungkin, muncul pada titik dan yang lain muncul pada sisi.
E(G) 
{1,2,…,p+q} sedemikian hingga bobot sisi, w(uv)=f(u)+f(v)+f(uv), uv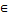 
E(G), membentuk barisan aritmatik dengan suku pertama a dan selisih tiap suku d. Suatu graf G adalah super jika label terkecil yang mungkin, muncul pada titik dan yang lain muncul pada sisi.
Dalam tulisan ini kita mempelajari pelabelan total super sisi antimagic untuk graf Tunas Kelapa tunggal Hasilnya menunjukkan bahwa graf tunas kelapa tunggal CRn,m mempunyai pelabelan total super sisi antimagic.
Kata-Kata Kunci : Pelabelan Titik (a,d)-sisi antimagic, Pelabelan Total Super (a,d)- Sisi Antimagic, Coconut Sprout Graph
INTRODUCTION
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A ”graph” in this context refers to a collection of vertices or ’nodes’ and a collection of edges that connect pairs of vertices. A graph may be undirected, meaning that there is no distinction between the two vertices associated with each edge, or its edges may be directed from one vertex to another. Graphs are one of the prime objects of study in discrete mathematics.
An (a, d)-edge-antimagic total labeling on a graph G is a bijective function f : V (G) ![clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgKewqv6tiq-9RLwu7B_4QjIipVngbzCf-8BA7bh4BAw-MlYStSH7FtyusBdDoJfLwFPth29ERR5d3_EG1kTXd3_igNjt_frDWpY3t5K3MOYDOFRNmg6K4GKay80vzgVGXELftNaNYb9qS7/?imgmax=800 "clip_image002[4]")
E(G)![clip_image004[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhCerALrADiAX-trpjK1Pqdoys7vMV0MGcdgZhV9YX-eVsYz_6gYsSxHH5pB6dQqoODHU1G3CroA2F6h52H8OIu9Ll4SP0Tv-iIFGatScmEhZ9_UYuKj_M2sQUF8Ul2L_RcOMpD6GE-4rDa/?imgmax=800 "clip_image004[4]")
{1, 2,..., p + q} g with the property that the edge-weights w(uv) = f(u)+f(uv)+f(v), uv 2 ![clip_image006[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEivniN8GNYrSsZOKFr719re_FheOQeSfcWZD2VVX6coh83eBx8xfh3dcPpxz6x19yL800f-ga5DTE1Wj9MCWws6ZP4_ZX3fwV3NydW9hecF5HPnNJr4ifSFClbiw92vXmV1WY6YRZQG_RvU/?imgmax=800 "clip_image006[4]")
E(G), form an arithmetic progression {a,a+d,a+2d,…,a+(q-1)d}. where a > 0 and d ≥ 0 are two fixed integers. If such a labeling exists then G is said to be an (a; d)-edge-antimagic total graph. Such a graph G is called super if the smallest possible labels appear on the vertices. Thus, a super (a, d)-edge-antimagic total graph is a graph that admits a super (a, d)-edge-antimagic total labeling.
![clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjXAYPzCC59zaXEBCGOAyasi-V9ZeCjTOpe_1GcbGc2AzfoXEwVyuxKC6Rz2kwPJZCjeeCfuTfFWlO46U55lkCeFQCKQahM2sKmT5a5wzQEfIWFB8OyHmgF0A-WTPStARAZYR6hHhynqAf0/s1600-h/clip_image002%25255B4%25255D%25255B2%25255D.gif "clip_image002[4]"){kind=small}
E(G)![clip_image004[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEilr2fY2b7ApK_VfatBohtIVsjSiG2qbcmTXgQK5f1GEmvq-TmmN8UabaVru96BcUNEisz3lr1E-WQzEr2XkapO0ZJnUjJe2kO1idN5kfiL3UEjacFzpdyFQK7MH25xu3BukS3auK8Dx-Rh/s1600-h/clip_image004%25255B4%25255D%25255B2%25255D.gif "clip_image004[4]"){kind=small}
{1, 2,..., p + q} g with the property that the edge-weights w(uv) = f(u)+f(uv)+f(v), uv 2 ![clip_image006[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOTsa1bQZFAs707INyA5Dif5HqloITVQaJ_1nPJYukwW2Vv8WmmIJyYEvgiHOsxR8_Y0OrMhrOQj3M4DrYijKW_CqrJHNJmPw5KvyFUq0ySKgKzho-VEa_p1Ojo1MUKwwrjfcVBtgfLX2t/s1600-h/clip_image006%25255B4%25255D%25255B2%25255D.gif "clip_image006[4]"){kind=small}
E(G), form an arithmetic progression {a,a+d,a+2d,…,a+(q-1)d}. where a > 0 and d ≥ 0 are two fixed integers. If such a labeling exists then G is said to be an (a; d)-edge-antimagic total graph. Such a graph G is called super if the smallest possible labels appear on the vertices. Thus, a super (a, d)-edge-antimagic total graph is a graph that admits a super (a, d)-edge-antimagic total labeling. 
The concept of (a,d)-edge-antimagic total labeling, introduced by Simanjuntak at al. in [14], is natural extension of the notion of edge-magic labeling defined by Kotzig and Rosa [1] (see also [4], [5] and [6]).
In this paper we investigate the existence of super (a,d)-edge-antimagic total labelings for connected and disconnected graphs. We will now concentrate on the connected coconut sprout denoted by CRn,m .
