Relasi antara Anggota Dua Himpunan

 

Relasi (hubungan) dapat terjadi antara anggota dari dua himpunan. Misalnya, A = {1, 2, 3, 4} dan B = {4, 5, 6, 7}. Antara anggota himpunan A dan B ada relasi “tiga kurangnya dari”. Relasi tersebut dapat ditunjukkan dengan diagram sbb:

Relasi antara anggota himpunan A dan B dapat dinyatakan sebagai himpunan pasangan berurutan sebagai berikut:{(1,4), (2,5), (3,6), (4, 7)}

Relasi antara anggota himpunan A dan B dapat dinyatakan dengan menggunakan rumus. Misalnya anggota A dinyatakan dengan x, maka pasangannya ialah y anggota B yang dapatdirumuskan:y = x + 3

Pengertian Relasi antara Anggota Dua Himpunan

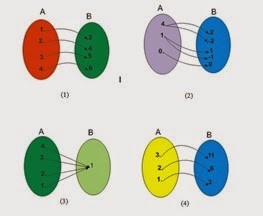
Perhatikan diagram panah berikut.:

Pada gambar 1, 3 dan 4 setiap anggota himpunan A mempunyai pasangan tepat satu anggota himpunan B. Relasi yang memiliki ciri seperti itu disebut fungsi atau pemetaan.

Pada gambar 2 bukan fungsi karena ada anggota A yang punya pasangan lebih dari satu anggota B.

Definisi:Relasi dari himpunan A ke himpunan B disebut fungsi atau pemetaaan, jika dan hanya jika setiap unsur dalam himpunan A berpasangan tepat dengan satu unsur dalam himpunan B.

Misalkan f adalah suatu fungsi dari himpunan A ke himpunan B, maka fungsi f dilambangkan dengan:

f: A-->B

Jika dan sehingga pasangan berurut maka y disebut peta atau bayangan dari x oleh fungsi f.

Peta atau bayangan ini dinayatakan dengan seperti ditunjukkan pada gambar berikut.

Jadi, suatu fungi f dapat disajikan dengan lambang pemetaan sebagai berikut:

dengan disebut rumus atau aturan fungsi, x disebut peubah (variabel) bebas dan y disebut peubah (variabel) tak bebas.

Himpunan A disebut daerah asal atau domain dan dilambangkan dengan D_f.

Himpunan B disebut daerah kawan atau kodomain dan dilambangkan dengan K_f.

Himpunan dari semua peta A di B disebut daerah hasil (range) dan dilambangkan dengan R_f.